There are three different concepts in the field of classical mechanics. These three concepts are energy, force, and potential.
These can be further discussed in Electrostatics. However, in this article, We will discuss what is electric potential.
What is Electric Potential (EP)
We can define it in a very simple way. It is the capability of the charged particles or body to perform work. During the charging of a body, either electron is removed from a body or injected into it. In both cases, the work is done. This work stores in the body in the form of electric potential (It is the same as voltage).
We can determine the potential from the capacity of the charged body for a single point. The electrical potential can be measured in the unit of volt. And we can derive the formula from Ohm’s law as :
V = I*R
While
- V is potential difference i.e Voltage in volt (V).
- I is the current drawn by the load in Amperes (A).
- R is the resistance of the load in Ohm (Ω).
Why is the potential difference important?
Potential difference is very important because it is the main factor that has made it possible for us to differentiate between static and dynamic electricity.
The “flow of charge” that is known to us as the current, shows dynamic electricity.
The potential difference has made the concept of the flow of charges possible. We know that everything that flows, flows from a higher position to a lower position.
Potential has values. It can be low and it can be high too. So, when there is a potential difference, the energy flows from the higher to the lower potential. Energy flows in the form of charges and the flow of charges is called current.
More is the potential difference; more will be the current. Let us understand this with an analogy. We all have seen a garden pipe and have done some fun with it too.
If we increase the water supply by steering the tap, the water flows through the pipe increases. The diameter of the pipe has related the resistance.
If the pipe has a larger diameter, it will be easier for water to flow through the pipe. If the resistance is lesser, it will be easier for the charges to flow through the wire. We studied that increasing the water supply increases the water, unintentionally we are increasing the pressure.
Increased pressure will push more water particles through the pipe if we keep the diameter the same. Similarly, the flow of current can be increased by increasing the potential difference while keeping the resistance constant.
To fill up a bigger flower pot, we need more amount of water otherwise our flowers will wither off. Similarly, if we need to power up a bigger electrical device, we need to supply more power.
That is possible by controlling the power and being able to increase the voltage or potential difference.
So, if you want to run your device properly, you need to have the knowledge of rated potential differences. That’s the reason potential difference is very important.
How is a potential difference created?
There are many ways to create a potential difference.
Let us start with a relatively newer and a little more fascinating technology known as solar power. Solar voltage/ potential differences generated by the solar cells or photovoltaic cells. The method of creation of potential difference is as:
- The sunlight energizes the electrons of a silicon atom.
- This energy can be used by the electrons to either move up to a higher energy level shell or just leave the atom and flow in the metal. In both cases, the energy of these electrons (potential) is increased.
- The potential of the energized electron is more than the other electrons. So, the potential difference is created
Another way to create the potential difference is by using a cell or a battery. A cell is a singular item while a battery may consist of multiple cells.
The chemical reaction happening inside the cell creates the potential difference at the terminals of that cell.
Certain types of materials such as silk, wool wax, hair with a comb, and others, when rubbed with each other, creates a potential difference.
When we rub two such bodies against each other the energy used in rubbing the objects energizes the objects.
This increases the potential of the objects. So, the other objects have a lower potential which creates a potential difference.
Unit of measurement
As we know that work can be measured in joules and the charge in coulomb. Therefore, the unit can be determined as Joules per Coulomb. And we also know that Joule per coulomb is the unit of Volt. So another unit of electric potential is volt.
What is Volt?: The electric potential will be one volt if One joule of work is done for charging a body for one coulomb.
In the above topic, we discussed EP for one point. Now let’s discuss it for two points. When we discuss two points we call it potential difference. And can be defined as the amount of work required to bring one unit positive charge from one point to other points.
When a body is charged, if the two positively charged can attract each other. Similarly, if the bodies are charged with a similar charge it will repulse each other.
When we connect two electrically charge bodies via an electrical conductor, the current flows. The current flows from high potential to Low Potential. And depending upon the resistance of the conductor and the potential difference between it.
Potential difference Formula in AC & DC circuits
DC and AC circuits are consists of power source, electrical conductor and load. The power source in DC circuits is either a DC generator or a battery. While in AC circuits the power source is AC generator (As we all know the AC power can’t be stored for later usage).
The main difference between DC and AC loads is the power factor. It always unity in DC loads while in AC loads power factor should be taken in account.
Voltage formula For DC circuits
From Ohm’s law VDC = P / I
while
- I is current in Amp.
- P is power in Watt.
- V is the potential difference in Volt.
Voltage formula For AC circuits
- For AC single phase circuits : VAC-1ø = P / (I*PF).
While
- V is the voltage (potential difference)
- P is the power
- PF is power factor
- For AC three phase circuits VAC-3ø = P / (√3*I*PF).
Measurements in Circuits
Using voltmeter we measure the voltage between any two points of the electrical circuits. The voltmeter is connected in parallel as in the below circuit image.
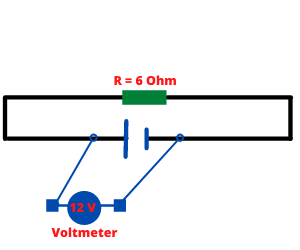
Important safety note: When using any Avometer to measure voltage make sure that the voltage range of the device is suitable for the circuit voltage. If the circuit voltage is higher than that of the measurement device this will cause device damage and may cause human injuries.
Example of electric potential calculation
Assume we have an electrical AC circuit. In this circuit we have power source of voltage V, and a single phase induction motor of 10 KW, current 53.4A, and power factor of 0.85 Calculate the voltage of the circuit.
Solution
using the formula of 1-phase voltage VAC-1ø = P / (I*PF)
V = 10000/(53.4*0.85) = 220 V
Now if the same example is for three phase induction motor with current of 16.9A, then, VAC-3ø = P / (√3*I*PF)
V = 10000/ (1.73*16.9*0.85) = 400V
Using android free application
Android free application “Fast electrical calculator” is easy to use app. It has the most popular electrical calculations which can be used in AC single and three phase circuit calculation.
Which one kills, Voltage (electric potential) or current?
This question is a famous one on social media pages. It seems confusing, But if we understand the electric chock we can answer it easily. The electric chock is the flow of electrical current through human body. But No voltage, no current!
This means that if the human body has no potential difference (voltage) then no current will flow, which means no electrical chock will occur. This is why birds don’t get chocked even they are on the energized wire. As there is no Voltage difference.
The current is the killer but the voltage is the cause. This means that current kills but it need Voltage to be able to flow through the human body breaking its resistance.
What is the difference between Voltage and Potential difference?
Potential difference is the difference in the energies of two points present in an electric field. The energy that a charged particle possesses due to its position in the electric field is its potential.
The difference in the potentials of the particles is called the potential difference. So, how is it different from the voltage, and if it is not why do we need voltage? The answer is that the voltage is the quantitative measurement of potential difference.
Voltage is normally defined as the quantity of difference of energies in terms of current and resistance. Otherwise, the potential difference is the same as the voltage. We know that the symbol to represent the potential difference is “V”.
Voltage is also represented by “V”. Both, potential difference and voltage, share the same unit that is Volts. But I just told you that the potential difference and voltage have different definitions.
So, there is no need to worry as the concept is the same but the way to describe both items is a little different. We know that the energy of every matter due to its position is defined as its potential energy.
We also know that the sub-atomic elements such as electrons, protons, and neutrons have mass as well as electric charges on them. Neutrons are electrically neutral but the electrons and protons are negatively and positively charged respectively.
So, protons and electrons need to have some work done to keep them apart otherwise the atom would collapse. That work done is the potential of the charged particles. Depending upon the shell of the electrons, it keeps energy.
The electrons revolving in the lowest energy-level shell/ orbit have the lowest energy. And it keeps on increasing from lowest to highest when we move from orbit 1 to 2, 3, and so on.
The concept we need to grab from this is that when an electron of an atom is residing in its 3rd orbit and another electron of the same or the other atom,they have different values of energy.
The potential difference between these electrons is more than the electrons of the same orbit. That is how we observe the potential differences.
While the voltage is observed in the sense that it pushes 1 ampere of current through 1-ohm resistance, it is calculated to be 1 volt. So, keeping both these examples, now you can see that both the terms are exactly the same but are used according to their respective context.
Why is electric potential always positive?
Before answering this question, this should be made clear that the discussion in this paragraph is purely about the electric potential and not the potential difference.
Electric potential is always positive. The reason for this quantity to be positive is that it is energy. Energy is not negative. The context of observing the energy level of a body may look like it is adding to the body or leaving the body.
If the energy is absorbed by the body, its energy level increases so do its potential. But if the body loses the energy, its energy level decreases and so does its potential. So, you may say that the energy was subtracted from the body.
One of the easiest methods to understand this is by remembering the concept of scalar quantities. Potential is a scalar quantity so is the distance. We cannot have a negative distance. Like we cannot say that today I walked -3kms.
But we can say that Ann walked 5 steps forward and then 1 step backward. Now we can see that Ann walked a total of 6 steps.
But the distance from his origin after coming 1 step back is just 4 steps. So, did we have a negative distance? No, all we have is just a change of perspective.
If I think of it as the total distance covered then it is 6 steps. But when I change my perspective and think of it as a distance from origin then it is 4 steps.
The steps that Ann walked forward and backward are 5 and 1 respectively. The key point in this analogy is that we did not have any negative distance.
Similarly, negative energy is never there. It is just a transfer of energy from a higher level to a lower level. So, we can say that the positive or negative sign is assigned according to the frame of reference.
Is electric potential a scalar or vector?
Electric potential is a scalar quantity. To prove that we have got the mathematical explanation of electric potential. The formula of electric potential is:
U=W/q
, where W is the work done on a unit charge to bring it from infinity to the electric field and q is the charge. Work is a scalar quantity, and so is the charge.
Work is defined to be W=F.S. which is the dot-product of Force and Displacement that results in a scalar quantity. Also, W/q also results in a scalar.
So, that proves it to be a scalar quantity.
Another use of Electric potential is given by Faraday’s law. It states:
∇*E=0
Where ∇ is the del operator and E is the electric field defined as:
E=-∇ф
, we know that ∇ operated on scalar quantities only. So, ф that is representing the electric potential, is a scalar quantity.
Why electric potential of Earth is taken as zero?
Let’s consider the Earth to be a capacitor. We need to add more and more charges to the capacitor to raise its voltage level.
Earth is the biggest and the most accessible item for human beings. So, if we want to raise the voltage level of the surface of the earth, we need so many charged particles that have no count.
So, due to the requirement of so much energy that has never been generated, the voltage of the earth is considered zero.
But we know that there are zillions of charges that are flowing into the earth every second. So, why does it not change the voltage level of the earth from 0 to a greater value? So, there are 2 answers to it.
One, we don’t know that all the charges that are flowing into the surface of the earth have the same polarity. Let us assume that a block of a town is flowing the negative charges into the ground.
And as we are assuming, it is safe to assume that the other town is flowing the same number of positive charges. But this is not a good explanation. If we look at the scientific side, let us see the formula of the electric potential of a sphere.
We know that earth is a big sphere. So, for its potential, we can use:
V = (k q) / r
, where k is the electrostatic constant, r is the distance between the interacting charges, q is the charge and V is the potential on the earth. The dividing figure “r” is always very much larger than the “q” that is being flowninto the sphere. So, the quantity V will keep on decreasing as the r increases.
Another explanation is that the potential of the earth is not absolute zero. It may have charges due to the metallic substances found in itself.
These metallic elements make it possible for the charges of the grounding wire to flow through them.Due to this, a little magnitude of potential exists on the surface of the earth. And also, if we realize, most of the time we measure the potential on a point with respect to earth.
That means if the terminal of the battery is at 5V, then it is 5V more than the potential of the earth. It is almost impossible to get rid of the effect of the potential of the earth on an object that is touching the ground.
Why is electric potential constant throughout a conductor?
We know that the electric potential is the work done in bringing a unit test charge from infinity to a certain point inside an electric field.
Let us take the example of a conducting sphere. This sphere has an electric field E. The electric field does not have any tangential component on its surface. This is a vector field that makes an angle of 90 degrees at every point on the surface of the sphere.
The direction of this vector field is outwards from the surface. As the tangential component is absent, there is no electric field present between two points on the surface of the sphere.
Assume two points A and B on the surface of the sphere. If we want to move a charge from point B to A, there is no work required to do so. Because there is no opposing force such as an electric field that makes it difficult for the charge to move on the surface from one point to the other.
All we need is some energy delivered to the surface that is changed to kinetic energy to move the charge. This surface is just as simple as a conductor with no electric potential at all, where the charges have free motion.
So, what we just proved is that there is no work required in moving a charge from B to A which implies that the electric potential on the surface is 0. We know that 0 is a constant.
So, the matter of surface is resolved and now let us see the potential inside the conductor. We all know that the electric field does not exist inside the conductor. On the surface, the electric field did not have any tangential component. But inside the conductor, there is neither the normal nor the tangential component is present.
So, here too, the electric potential is 0.
The last confusion which we must get rid of is if we increase the supply of energy at one end of the conductor, then the other end should have a different electric potential. That means the potential of a conductor is variable.
Well, addressing this situation we can say it is true but only for a moment. Conductors have equipotential surfaces which means an increase in energy is distribute all over the surface. If we increase the supply of energy at one end, for a moment its potential will increase.
But after that moment, that a very-very short interval of time, this increased potential will be distributed all over the conductor. Just like heat does. So, the potential at all the points becomes uniform.
So, we have proved that the potential is always constant throughout the conductor.
Can Electric potential be zero while the electric field intensity is non-zero?
Yes. It is possible that the electric field intensity is non-zero while the electric potential is zero at the same time.
We know that each electric charge has electric field lines coming in to or going out from the center of the charge. It depends upon the polarity of charge. Let us take spherical charges. If it is a positive charge then the electric field lines will originate from the center of the charge towards the outside.
If it is a negative charge, the electric field lines will be directed towards the center of the charge. If 2 charges of equal magnitude but opposite polarity are brought closer, the electric field lines will be originating from the positive charge and will exit into the negative charge.
The point in between the charges has zero potential. While the electric field lines exist at that point. Because the charges get canceled out. Now the only way to find out whether the charges have canceled out each other or not is to take a test charge in that region.
If the test charge (test charges are normally positive charges) moves freely independent of both charges (those charges who have made this 0 potential region), then the potential is 0.
But if the charge is deflected towards the negative side, the positive charge is exerting a columbic force on this test charge. But if the deflection is towards the positive side, the negative charge affects its course of action.
potential difference in parallel and series combinations
The electric potential throughout a conductor is constant. If we connect a conductor to a battery source’s positive. It will attain the potential of the positive terminal of the battery.
Because the connection makes the wire and the terminal of the battery behave as a single conductor. Also, if we connect a wire with the neutral terminal of the battery, the whole wire will behave just like the neutral terminal of the battery.
We know that potential is the measure of the energy of an object. More the energy carriers (electrons/ holes) are in a conductor, the higher will be the potential of the conductor. Let us take a simple resistive circuit with only 2 resistors of the same values.
In the parallel combination, the terminals of the battery are directly connected with the terminals of the resistors. One of the terminals of both resistors will have exactly the same potential as the positive terminal of the battery.
The same is the case for the negative terminal. So, the potential difference between the positive and negative/neutral terminals of the resistors is as same as the potential difference between the terminals of the battery.
In the case of the series combination, there is only one pathway for the electrons. We know that the potential is the push that pushes the electrons through the circuit.
If we keep increasing the components one after the other in the series, the push will keep decreasing.
Water examples always come in handy to explain the current. Assume that the battery is the dam. The pressure of water is the potential and the volume of water is the current.
The cross-sectional area of passages that lead to canals is related inversely to the resistance. (More the cross-sectional area lesser will be the resistance).
If two canals have equal cross-sectional areas for the water from the dam, the pressure of water is equal in both canals. On the other hand, if canal A (directly connected to the dam) is watering another canal B (connected to the dam via canal A), the pressure will decrease in canal B.
What is the relationship between current and potential differences?
Ohm’s law perfectly describes the relationship between the current and voltage/potential difference. It states that the current through a component is directly proportional to the potential difference across that component.
More is the potential difference more will be the current flowing through the component and vice versa.
Mathematically:
IαV
, where α is the proportionality constant.
Another way to explain the relationship between the current and voltage is by the cause-and-effect scenario.
Voltage is the cause and electric current is the effect. In the absence of the voltage, current would not exist. Potential difference makes the charges flow from the region of the higher potential to a region of lower potential.
And we know that the current is actually the flow of charges. This means if there is no imbalance of the potential, charges will not flow and ultimately, the current would not exist.
The potential difference across the resistors and examples.
The potential difference in the parallel combination of resistors is the same. According to ohm’s law:
V=IR,
But if there are multiple resistances in the circuit, then the method to calculate the equivalent resistance.
In the parallel circuit, to calculate equivalent resistance, we have to add the inverses of all the resistances and then take the inverse of this sum. Let’s say that we have 2 resistors R1 and R2 connected in a parallel combination.
To calculate the equivalent resistance, we have the formula:
1/Req=1/R1+1/R2
Or, Req= (R1R2)/(R1+R2)
As, the voltage across both resistors is the same and there is no other component except these resistors, the voltage across both resistors will be the same as the applied voltage.
V=V1, V=V2, V1=V2
Let us now assume that these resistors are in a series combination. The sum of resistances in the series is the equivalent resistance of the circuit. So,
Req= R1+R2
The voltage across each resistor is different. But the current is constant. So, we can use current to find the voltage across the resistors.
V1=IR1, V2=IR2 while, I=I1=I2
What is the relation between electric field and electric potential?
The electric field can be defined as the negative gradient of electric potential. To prove that we need to define 2 equipotential surfaces.
Where surface 1 has the potential of V and surface 2 has the potential of V. dv. While the distance between these surfaces is dx.
Let an electric field of E be present perpendicular to both these surfaces. The force that is exerted on a positive charge q is given as:
F = q E……… (a)
Where q is the magnitude of the charge and E is the electric field intensity.
We know that “the potential is the work done in bringing a unit positive charge from infinity (point B) to a point (point A) in the Electric field.
WBA= VA-VB
Or WBA =VA-(VA-dv)
Or WBA=dv…… (b)
Let us suppose, for the purpose of simplification, the magnitude of charge q is 1C. So, equation (a) can be written as:
F=E ……… (1)
The work done in bringing this q=1C from infinity to a point in electric field E is:
W=F. dx
, where the charge moves for a distance of dx.
We also know that the sine component of the work does not affect the value of work. So, the equation written above can be written as:
W=F. dx Cos(θ)
, where θ is the angle and its value is 180 degrees.
So, the equation above becomes:
W=F. dx (-1)
Using eq (1),
W=-E dx
Using the equation (b):
dv =-E dx
or dv/dx=-E
or E =-del(V)
, where del operator is used to calculate the partial derivative of the V with respect to the variables of the plane. The above-written equation describes the first statement of this answer as the negative gradient of electric potential is the electric field.
How the potential difference can be increased in a circuit?
Potential differences can be increased in a circuit by providing more energy to the circuit. First, we need to grasp how the potential difference comes into existence then we will be able to learn how the potential difference can be varied to be increased.
When the chemical reaction takes place in a circuit the potential on one of the terminals increases due to the deposition of more and more energy carriers at that terminal.
While the potential of the other terminal remains the same. So, a difference in potential comes into existence.
If we connect an electrical component across these terminals, the charges will flow from the higher potential to the lower potential (the conventional approach of charges is being used).
If somehow, the deposition of charges is increased on the higher potential terminal there will be more charges available at this terminal than before.
Similarly, the potential difference will also increase due to more and more charges at one terminal and lesser charges at another end.
In the DC circuits, the potential difference can be increased by using higher voltage batteries. In AC circuits, if the movement of the conductor is increased in the magnetic field (increasing the frequency) or vice versa, the voltage supply is increased.
How does temperature affect the potential difference?
In a galvanic cell:
The voltage/ potential difference of the galvanic cells decreases as the temperature increases. A range of experiments was performed by Walther Nernst and he derived Nernst’s equation:
E cell=E0cell – [((RT) / (z F)) x ln (Q r)]
, where E0cell is the electric potential by the battery at standard conditions i.e., 250 and 1mol/ ltr
, E cell is the electric potential at a certain temperature
, R is the universal gas constant
, z is the number of moles per reaction
, F is the faraday’s constant
, Q r is the reaction constant
, and Tis temperature and its unit is Kelvin.
If we analyze the equation, we can see the (-) sign on the second term. That indicates that the potential will decrease if the T is increased. While the values of R and F do not change and z and Q r are also kept the same.
In a battery/ conductor:
In a battery too, the voltage decreases with the increase in temperature. The increase in temperature increases the resistance and makes it difficult for the energy carriers to flow through the conductor. So, the voltage decreases.
