Blog

What is Ohm’s law? examples and calculator

What is Ohm’s law?

Ohm’s Law is a fundamental principle in electrical engineering that defines the relationship between voltage, current, and resistance in an electrical circuit. It states that:

V = I×R

Where:

  • is the voltage across the conductor,
  • is the current flowing through the conductor, and
  • is the resistance of the conductor.

Explanation:

  • Voltage (V): The potential difference or “push” that drives electrons through a circuit.
  • Current (I): The flow of electric charge in the circuit.
  • Resistance (R): The opposition to the flow of current, caused by the material or components in the circuit.

Key Points:

  • If the resistance in a circuit is constant, the current is directly proportional to the voltage.
  • Increasing the voltage increases the current, and increasing the resistance reduces the current.
  • Ohm’s Law applies to many electrical circuits, but not to non-linear devices where the relationship between voltage and current isn’t consistent (e.g., diodes).

Ohms Law Triangle

If we transpose a standard equation of Ohm law using a triangle. It gives us a combination of different values.

Ohm's law triangle
Ohm’s law triangle

For finding different combinations we can use the triangle to simplify the formulas.

Ohm’s law examples

Assume we have an electrical circuit. In this circuit, we have a battery of 12 V and a load of 6 Ω resistance. Calculate the current which should pass through the load.

 

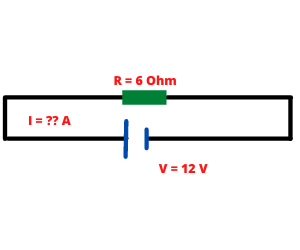
Ohm's law example
Ohm’s law example

Using Ohm’s law formula we can find the current as follows: I = V/R = 12 / 6 = 2 A

Now the same law is applicable to find the value of both resistance and voltage.

Assume the same circuit with the same voltage and the current passing through the load is 2 A. We need to calculate the value of the load resistance.

Using the same Ohm’s formula we can find the resistance as follows: R = V/I = 12 / 2 = 6 Ω Assume the same circuit with the same resistance and the current passing through the load is 2 A. We need to calculate the value of the battery voltage.

Using the same Ohm’s formula we can find the voltage as follows: V = I*R = 2*6 = 12 V In this way, we calculated all parameters of the electrical circuit simply by using Ohm’s law formula.

is Ohm’s law universal?

No, Ohm’s Law is not universal. It applies only under specific conditions and for particular materials known as ohmic materials, where the relationship between voltage (V), current (I), and resistance (R) is linear. Here’s why it is not universally applicable:

Limitations of Ohm’s Law

  1. Non-Ohmic Materials:

    • Some materials, like semiconductors (e.g., silicon) or gases (e.g., in discharge lamps), have a non-linear voltage-current relationship, meaning their resistance changes with applied voltage or current.
    • Example: Diodes and transistors do not obey Ohm’s Law because their current depends exponentially on the applied voltage.

  2. Temperature Dependence:

    • For many materials, resistance changes with temperature. For instance:
      • Metals: Resistance increases with temperature.
      • Superconductors: Below a critical temperature, they exhibit zero resistance, violating Ohm’s Law.

  3. High-Frequency Circuits:

    • In alternating current (AC) circuits, especially at high frequencies, additional factors like reactance (inductive and capacitive) come into play, making Ohm’s Law insufficient to describe the circuit behavior.

  4. Extreme Conditions:

    • At very high voltages (e.g., in electrical arcs) or under extreme pressures, materials may not behave in ways consistent with Ohm’s Law.

Does Ohm’s law applicable to liquid electrolytes?

Yes, Ohm’s Law is applicable to liquid electrolytes, but with certain considerations and limitations. Electrolytes, such as saltwater or acid solutions, conduct electricity via the movement of ions rather than electrons.

While the basic principle of Ohm’s Law can still describe the relationship between voltage, current, and resistance in electrolytes, there are factors unique to electrolytes that can affect its applicability:

Factors Affecting Ohm’s Law in Electrolytes

  1. Ion Movement Instead of Electrons:

    • In electrolytes, current is carried by positively and negatively charged ions.
    • Resistance in electrolytes is influenced by the concentration and mobility of these ions.

  2. Temperature Dependence:

    • The resistance of electrolytes decreases as temperature increases because ion mobility improves at higher temperatures.

  3. Concentration of Electrolyte:

    • Higher ion concentration reduces resistance, increasing conductivity.
    • For very dilute or highly concentrated solutions, the relationship may deviate slightly from linearity.

  4. Electrode Polarization:

    • In practice, the electrodes in contact with the electrolyte can polarize during current flow, creating an additional voltage drop that complicates measurements.

  5. Non-Ohmic Behavior:

    • At high currents or voltages, some electrolytes may exhibit non-linear behavior due to electrochemical reactions (e.g., electrolysis or gas generation).

Conclusion

Ohm’s Law applies to liquid electrolytes for small applied voltages and currents under steady-state conditions. However, deviations can occur due to electrode effects, chemical reactions, and other factors. For precise studies of electrolytes, concepts like ionic conductivity and the resistivity of the electrolyte solution are often used alongside Ohm’s Law.

Don’t Leave Empty-Handed!

Install my Free Android App on Google Play:

Electrical Cables Most Common Tables “Cables Tables”

And, my Electrical Calculations App “Fast Electrical Calculator”

Discover more great content by subscribing to My channel

Looking to stay ahead of the game in the world of electrical engineering? Subscribe to my YouTube channel and gain access to exclusive content you won’t find anywhere else!

The staff I recommend

(Amazon Affiliate Links to products I believe are high quality):

Disclaimer: This contains affiliate links to Amazon products. I may earn a commission for purchases made through these links.