Difference Between Resistors in Parallel and Series

Different types of conditions are observed while connecting resistors in parallel and series.

The connection type of resistors affects the current, voltage, and total resistance value. Let’s discuss the characteristics of connecting resistors in parallel and series

Table of Contents

resistors in parallel vs series

Resistors in series and parallel are two basic configurations in which resistors can be connected within an electrical circuit, each with its own unique properties and applications.

here’s the information organized in a table format:

Properties	Resistors in Series	Resistors in Parallel
Current	The same current flows through all resistors	Total current is the sum of the currents through individual resistors
Voltage	Total voltage is the sum of individual voltages	The voltage across each resistor is the same and equal to the total voltage
Equivalent Resistance	Equivalent resistance is the algebraic sum of individual resistance	The reciprocal of the equivalent resistance is the sum of the reciprocals of individual resistances
Applications	Voltage dividers, where the input voltage is divided	Circuits requiring different resistance values for different branches or components

Resistors in parallel vs series

Choosing between series and parallel connections depends on the specific requirements of the electrical circuit.

Series connections are useful for obtaining specific voltage splits, while parallel connections are often used when different resistances are needed for different branches or components in a circuit.

What are Resistors in Parallel Combination?

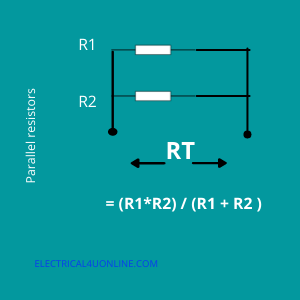
Resistors in parallel combination refer to a configuration where multiple resistors are connected across the same two points, allowing multiple paths for the current to flow.

In a parallel combination, the voltage across each resistor is the same, but the current divides among the resistors according to their individual resistances.

The total resistance $R_{eq}$ of $n$ resistors () connected in parallel can be calculated using the formula:

1/R eq =1/R 1 +1/R 2 +1/R 3 +\dots+1/R n

where is the sum of the reciprocals of the individual resistances.

The total resistance of a parallel combination is always smaller than the smallest individual resistance in the combination. This is because the parallel configuration provides multiple paths for the current to flow, reducing the overall resistance.

Additionally, in a parallel combination, the total current flowing into the combination is equal to the sum of the currents flowing through each individual resistor. The voltage across each resistor in a parallel combination remains the same.

resistors in the parallel connection formula

Resistors in Parallel Formula: The equation 1/R_eq=1/R₁+1/R₂+1/R₃+…+1/R_nis used to find the equivalent resistance R_T of (n) number of resistors connected in parallel combination in an electrical circuit.

This equation signifies that the reciprocal of the equivalent resistance (R_eq) is equal to the sum of the reciprocals of the individual resistances.

Once you find the sum of the reciprocals, take the reciprocal of the sum to obtain the equivalent resistance. This formula is widely used to determine the overall resistance when multiple resistors are connected in parallel.

In a parallel arrangement, if two resistors are equal, i.e. having the same value, the equivalent resistance R_T will become equal to R/2 i.e. half of the resistance of one resistor.
In the case of three equal resistors equivalent resistance R_T will become R/3 and so on. The main point to note is that the equivalent resistance is always less than the resistance of the smallest resistor in the circuit connected in a parallel combination.
Due to this the equivalent resistance R_twill decrease with the increase in the number of parallel resistors.

Resistors in Parallel Formula Examples

Example 1:

Assume an electrical circuit has two parallel resistors R1 = 10 Ohm & R = 20 Ohm, The equivalent resistance of the circuit will be Rt = 1/ ((1/10) + (1/20)) = 6.7 Ohm.

Example 2:

Assume R1 = 100 Ohm & R = 100 Ohm, The equivalent resistance of the circuit will be Rt = 1/((1/100) + (1/100)) = 50 Ohm.

Example 3:

Let’s consider three resistors in parallel, , , and . Applying the formula for the equivalent resistance:

Substitute the given values:

What Are Resistors in Series?

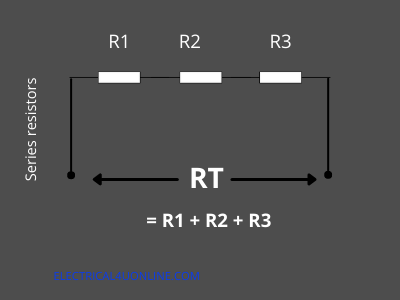
Resistors in series refer to a configuration where multiple resistors are connected end to end, forming a single path for the current to flow.

In this setup, the current passing through each resistor is the same, but the voltage across each resistor can differ, depending on their individual resistance values.

In this combination when the current follows from one resistor it has no path to go except passing from the next resistor.

What Is The Current In Series and Parallel Resistors?

In parallel circuits, the current across each branch is different, but the total current flowing into the parallel combination is the sum of the currents through the individual branches.

This principle follows from Kirchhoff’s current law, which states that the total current entering a junction must equal the total current leaving the junction.

For a series circuit, the current remains the same throughout the entire circuit. This is a consequence of Kirchhoff’s voltage law, which states that the total voltage around a closed loop must be zero.

Parallel Circuits:
- The current through each branch is determined by the voltage across that particular branch and the resistance of that branch (according to Ohm’s law, I=V/R).
- The total current flowing into the parallel combination is the sum of the currents flowing through the individual branches.
Series Circuits:
- The current remains the same throughout the entire circuit.
- The voltage across each component is determined by the product of the current and the resistance of that component (according to Ohm’s law, V=IR).

Understanding these principles is crucial for analyzing and designing electrical circuits.

For example, Let’s say R₁, R₂, R₃, and R4 are the resistors connected in series with current I_R1, I_R2, I_{R3 &}I_R4 respectively passing through them.

If 5A of current is passing through the resistor R₁ then I_R1 = I_R2 = I_R3= I_R4 = 5A

How to Calculate Resistors in Series?

As the current passes through each resistor is the same in the amount due to series combination the equivalent resistance will be the sum of the resistances of all the resistors connected together in series.

For example, Let us consider the four resistors connected in series with resistances R₁, R₂, R₃, and R₄respectively. Now the equivalent resistance R_T will be R_{T =}R₁ + R₂ + R₃+ R₄

The equivalent resistance may be defined as the value of resistance which can be used for all the resistors in series if a circuit without changing the value of
current and voltage.

Resistors in Series Formula Examples

Example 1:

Assume an electrical circuit has two parallel resistors R1 = 10 Ohm & R = 20 Ohm, The equivalent resistance of the circuit will be Rt = 10 + 20 = 30 Ohm.

Example 2:

Assume R1 = 100 Ohm & R = 100 Ohm, The equivalent resistance of the circuit will be Rt = 100 + 100 = 200 Ohm.

Voltage in Series and parallel Resistors

In electrical circuits, the distribution of voltage across resistors depends on the configuration of the circuit, whether the resistors are connected in series or in parallel.

Series Circuits:
- In a series circuit, the total voltage is the sum of the individual voltages across each resistor.
- The voltage across each resistor depends on its resistance and the current flowing through it. According to Ohm’s law, V=IR, where V is the voltage across the resistor, II is the current flowing through the resistor, and R is the resistance of the resistor.
- The total voltage of the series circuit is the sum of the voltages across each individual resistor.
Parallel Circuits:
- In a parallel circuit, the voltage across each branch is the same. This is a consequence of the fact that all components in parallel have the same voltage drop across them.
- Each branch in a parallel circuit can have a different current, but the voltage across them remains constant.
- The total current supplied to the parallel circuit is divided among the branches according to their resistances.

Understanding these principles helps in understanding how voltage is distributed in different types of circuits and aids in the analysis and design of electrical circuits.

Read My Other Article: What is Ohm’s Low?

Install my Free Android App on Google Play:

Electrical Cables Most Common Tables

And, my Electrical Calculations App “”

Discover more great content by subscribing to My channel

Looking to stay ahead of the game in the world of electrical engineering? Subscribe to my YouTube channel and gain access to exclusive content you won’t find anywhere else!