What Is Apparent Power? Definition And Formula

Table of Contents

What Is Apparent Power?

Apparent power is a term used in the field of electrical engineering and power systems. It represents the total power in an electrical circuit, taking into account both the real power and the reactive power.

In an alternating current (AC) circuit, the power can be divided into two components: real power and reactive power. Real power, measured in watts, represents the actual power that is converted into useful work, such as generating heat, light, or mechanical power. Reactive power, measured in volt-amperes reactive (VAR), is the power that flows back and forth between the source and reactive elements in the circuit, without being used to do any real work.

The apparent power, measured in volt-amperes (VA), is the combination of both the real power and the reactive power. It is the vector sum of the real power (the actual power that is consumed in the circuit) and the reactive power (the power oscillating back and forth between the source and the load).

Apparent power is important in power systems because it determines the sizing of equipment such as transformers, generators, and transmission lines. In practical terms, it represents the total power that must be supplied to a circuit to ensure the proper functioning of electrical equipment and devices.

apparent power formula

The basic formula for calculating apparent power for any circuit is:

The apparent power formula single phase S = V*I
The apparent power formula three phase S = √3 *V*I

The apparent power Unit is Volt Ampere (VA). If the apparent power in the electric circuit is supplied from a power supplier to the grid. It includes both real & reactive power consumption in the loads.

With the help of the power triangle formula, which shows the relationship between apparent, active, reactive power, and power factor we can find another apparent power formula as follows.

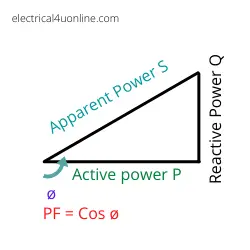
Power factor triangle — power triangle formula

From the power triangle we find S = √ (Active Power² + Reactive Power²)

S = √(Q² + P²)

where

$S$ is the apparent power in volt-amperes (VA)
Q is reactive power consumption in load (VAR)
P is active power consumption in load (W)

apparent power calculation Example

Assume we have a three-phase 10 KW load working on a 400 Volt power source. This Load has a 0.85 power factor. We need to calculate the apparent power of this load.

In this example, we have the load active power which is 10 KW, And the power factor of the load is 0.85 we calculate the current first as follows

P = √3 V * I * PF ⇒ I = P / (√3 *V * PF ) = 10,000/(1.73*400*0.85)

I = 17 A

Then, S =√3 V * I

S = 1.73*400*17 = 11.7 KVA

Note that, the active power is greater than the apparent one. This means that this load draws reactive power.

This is clear as the PF is 0.85 (the lower the power factor, the smaller the active power), For more information, read my article about factors that affect apparent power here.

Could S(KVA) be less than P(KW)? S is either less than or equal to P. In the case of unity PF the two powers are equal.

Why Is Apparent Power Important?

Apparent power is important in electrical systems for several reasons:

Sizing of Equipment: Apparent power helps in determining the capacity and sizing of electrical equipment such as transformers, generators, and transmission lines. Properly sizing equipment ensures that it can handle the expected loads without becoming overloaded or inefficient.
Efficiency Analysis: Understanding apparent power is crucial for evaluating the efficiency of power systems. By comparing the apparent power to the real power, engineers can assess how effectively power is being utilized within a system. Discrepancies between the two may indicate issues such as power losses or poor power factor.
Voltage Regulation: Apparent power is essential for maintaining stable voltage levels in power distribution systems. By accurately estimating the apparent power requirements, engineers can design and manage systems that ensure consistent and reliable voltage levels for consumers.
Power Factor Correction: Apparent power is closely related to power factor, which is a measure of how efficiently power is being used in a system. Monitoring and adjusting the power factor through methods such as power factor correction capacitors can help improve the overall efficiency of power systems, reduce energy consumption, and lower electricity costs.
Prevention of Overloading: Understanding apparent power helps in preventing overloading of electrical equipment. By considering both the real and reactive power components, engineers can ensure that the system is capable of handling the total power demands, thereby preventing equipment failures and minimizing downtime.
Billing and Cost Management: Apparent power is often a factor in determining electricity bills, especially for commercial and industrial consumers. Understanding and managing apparent power can help consumers optimize their power usage to avoid excessive charges and improve cost management.

By considering apparent power alongside real power and reactive power, engineers and system operators can design, operate, and maintain electrical systems more efficiently, ensuring reliable power delivery, minimizing losses, and optimizing energy usage.

Delve into the Intriguing World of Apparent Power and its Crucial Role in Modern Energy Systems! with Our In-Depth Article The imporance of apparent power!

What Are The Applications of Apparent Power?

Apparent power has several practical applications in various fields, particularly in electrical engineering and power systems. Some of the key applications of apparent power include:

Power System Design: Apparent power is crucial in the design of electrical power systems, helping engineers determine the appropriate ratings for equipment such as transformers, generators, and transmission lines.
Load Management: Understanding apparent power allows for effective load management in power distribution systems, enabling operators to balance the supply and demand of power more efficiently.
Power Factor Correction: Apparent power is closely related to power factor, so it is essential in implementing power factor correction techniques to improve the efficiency of electrical systems, reduce energy consumption, and optimize power usage.
Electrical Equipment Sizing: Apparent power helps in sizing electrical equipment to ensure that it can handle the expected loads without becoming overloaded, thus preventing equipment failures and ensuring reliable operation.
Voltage Regulation: Apparent power is used to regulate voltage levels in power distribution systems, helping to maintain stable and consistent voltage for consumers and preventing voltage fluctuations that could potentially damage electrical equipment.
Power Quality Analysis: Apparent power analysis is a part of assessing power quality in electrical systems, helping to identify issues such as voltage fluctuations, harmonics, and other power-related anomalies.
Energy Billing and Cost Management: Apparent power is a factor in determining electricity bills, especially for commercial and industrial consumers. Understanding and managing apparent power is crucial for optimizing power usage and avoiding excessive charges.
Renewable Energy Systems: Apparent power plays a significant role in the integration of renewable energy sources into the grid, as it helps manage the variability and intermittency of power generation from sources like solar and wind.

By considering apparent power in these applications, engineers and operators can ensure the efficient and reliable operation of electrical systems, optimize energy usage, and manage costs effectively.

For more information about Apparent power Applications, read my article here.

Differences Between Apparent Power and Real Power

Apparent Power	Real Power
Apparent power is the combination of both real and reactive power. Total Power in a circuit dissipated and returned power.	The actual amount of dissipated or used power in the circuit is usually called real power
Apparent power is symbolized by the capital S	Real Power is symbolized by the capital P
The unit of Apparent power is Volt Ampere(VA)	The unit of Real Power is a Watt
Apparent power in a circuit is actually the function of the circuit’s total impedance	Real power in a circuit is actually the function of the circuit’s dissipative elements and usually, it is Resistance
Apparent power is the product of the root mean square(RMS) values of the current and voltage	Real power is the product of the instantaneous values of the current and voltage in the circuit
In the AC Circuits, the total flow of the electric power is apparent power whether useful or not useful.	The portion of the total power(apparent power) which does the useful work in the system is a real or active power
The apparent power formula is *S = V I**	The real or active power formula is P = V I cos ø

Which Is Greater, Apparent, Or Real Power?

In an electrical system, apparent power can be greater than real power. This situation typically occurs in systems with reactive power components, such as circuits with inductive or capacitive loads.

Real power represents the actual power that is converted into useful work, while apparent power represents the total power in the circuit, considering both the real power and the reactive power.

Reactive power does not perform any actual work but is necessary for the establishment of electromagnetic fields in inductive or capacitive elements. As a result, in systems with reactive components, the apparent power (the combination of real power and reactive power) will be greater than the real power alone.

The relationship between apparent power (S), real power (P), and reactive power (Q) can be expressed using the equation:

S²=P²+Q²

This equation is known as the power triangle in the field of electrical engineering. It illustrates the relationship between the three types of power in an electrical system. If the circuit has a non-unity power factor (which indicates the presence of reactive power), the apparent power will be greater than the real power.

I have written a detailed article about Power Factor Correction, you can check it for more information.

Why Is Apparent Power Always Positive?

Apparent power is always considered positive because it represents the total power in an electrical circuit, taking into account both the real power (the power that is actually consumed in the circuit) and the reactive power (the power oscillating back and forth between the source and the load). It is essentially the magnitude of the complex power in an AC circuit.

Mathematically, apparent power is the vector sum of real power and reactive power. It is represented as the absolute value of the complex power, which means it is always positive. By taking the absolute value, the direction of the power flow is not considered, and only the magnitude is taken into account.

In practical terms, the concept of apparent power being positive is a result of how power is defined and measured in electrical systems.

It helps engineers and operators understand the total power requirements of a circuit, enabling them to properly size equipment, ensure efficient power transmission, and maintain the stability and reliability of the electrical grid.

Do You Pay Electricity Bill For Real Power Or Apparent Power?

You are typically billed for the real power consumed, not the apparent power. The unit of real power is the watt (W), and it represents the actual power that is consumed by the electrical devices in your home or business.

Real power is the component of the apparent power that performs useful work, such as generating heat, light, or mechanical power.

Apparent power, on the other hand, is the combination of both real power and reactive power. It is measured in volt-amperes (VA).

While it represents the total power in the circuit, including the power that flows back and forth between the source and reactive elements, it does not directly represent the actual energy consumed by the devices.

Electricity companies generally bill customers for the real power consumed, which is determined by the reading of the electric meter in units of kilowatt-hours (kWh). This is the product of the real power (in kilowatts) consumed and the duration of consumption (in hours).

Calculate Current From The Apparent Power.

Apparent power is the product of the RMS values of the current and the voltage. If voltage and apparent power values are given then current can be calculated.

Apparent Power – Single Phase Formula:

S = V * I

(Current) I = (Apparent Power) S / (Voltage) V

I = S / V = √ (P² + Q²)/ V

Apparent Power – Three-Phase Formula:

S = √ 3 *V * I

I = S / √ 3 V

Note: S is the apparent Power in VA

This equation shows that if the value of the real or active power, reactive power, and voltage is known then the current value can be calculated.

Calculating Current From The Apparent Power Example:

One of the most common examples of this calculation I face in my work is Transformer Current calculations. You know, transformer power is given in KVA, i.e in apparent power, In this case, we use the formula:

I = S / V

Calculate the current of a three-phase transformer of 100KVA Power and 400V voltage.

Transformer Current (I) = Apparent Power (S)/Voltage (V)

I = (100*1000) / (√ 3 * 400) = 144.34 A

Can you measure Apparent Power?

Yes, apparent power can be measured. Apparent power is that energy that you actually measure during the operation of an electrical system.

In simple words, Apparent power is actually the rated voltage times the rated current. We measure voltage and current by a multi-meter, voltage is measured in parallel and current in series, and multiplying them gives you the apparent power.

Apparent power is actually the power that a power source supplies to a load like a motor, However, the load only uses the real power, it’s the result of multiplying the voltage and current of the load.

Apparent power is measured in Volt Ampere (VA)and it is denoted by the capital letter S.

Why is the apparent power used in sizing generators?

Apparent power is used in sizing generators because it represents the total power in an electrical circuit, which includes both the real power (the power that is actually consumed by the load) and the reactive power (the power required to maintain electromagnetic fields in inductive or capacitive elements).

Sizing a generator based on apparent power ensures that the generator can meet the total power demand of the system, including both the active and reactive power components.

Here are some reasons why apparent power is used in sizing generators:

Total Power Demand: Apparent power provides a comprehensive measure of the total power requirements of a system, allowing for the selection of a generator that can meet both the real and reactive power needs of the load.
Capacity Considerations: Generators need to be appropriately sized to handle the peak apparent power demand of the system, ensuring that the generator can provide sufficient power under varying load conditions without becoming overloaded.
Reactive Power Compensation: Sizing based on apparent power helps account for the reactive power requirements of the system, enabling the generator to adequately supply the reactive power needed by inductive or capacitive loads without causing power factor issues or system inefficiencies.
Stability and Reliability: Properly sizing the generator based on apparent power ensures the stability and reliability of the electrical system, preventing issues such as voltage fluctuations, power factor problems, and equipment overloading.

By considering apparent power in the sizing of generators, engineers and system designers can ensure that the generators are appropriately rated to meet the total power demands of the connected loads, thereby maintaining the stability, efficiency, and reliability of the overall electrical system.

Does the generator produce apparent power?

Yes, a generator produces apparent power. In electrical engineering, a generator is a device that converts mechanical energy into electrical energy. When a generator is connected to a circuit, it supplies both real power and reactive power to the system, resulting in the production of apparent power.

The apparent power generated by the generator is the total power output that includes both the real power, which is the useful power that performs work, and the reactive power, which is necessary for establishing and maintaining electromagnetic fields in inductive or capacitive elements within the system.

The apparent power output of the generator is an important parameter to consider when evaluating the capacity and capability of the generator, as it indicates the total power that the generator can supply to the connected electrical system.

What do you mean by a power triangle?

A power triangle is a graphical representation used in electrical engineering to visualize the relationships between real power (P), reactive power (Q), and apparent power (S) in an AC circuit.

It is a way to illustrate these power components and their respective magnitudes and phase differences. The power triangle helps in understanding the power relationships in a circuit where there might be a phase difference between voltage and current.

In the power triangle:

The horizontal component represents real power (P), measured in watts (W). It indicates the actual power that is consumed in the circuit and performs useful work.
The vertical component represents reactive power (Q), measured in volt-amperes reactive (VAR). It represents the power that flows back and forth between the source and reactive elements in the circuit, without performing any actual work.
The hypotenuse of the triangle represents the apparent power (S), measured in volt-amperes (VA). It is the combination of both the real power and the reactive power and represents the total power in the circuit.

The power triangle equation is S²=P²+Q² The power triangle is a useful tool for visualizing the power relationships and understanding concepts such as power factor, which is the cosine of the angle between the real power and the apparent power.

For more information about Power Factor read my article Power Factor Correction, 8 Important Answers.

Is the rated power input the same as the apparent power?

The rated power input and the apparent power are not necessarily the same, although they can be related.

The rated power input refers to the maximum power that a device, such as a motor or an appliance, is designed to handle or consume. It is the power at which the device is expected to operate optimally and safely under normal conditions. This rating is often provided by the manufacturer and is an important specification to consider when selecting and using electrical equipment.

On the other hand, the apparent power is the total power in an electrical circuit, including both the real power and the reactive power. It is measured in volt-amperes (VA). Apparent power represents the magnitude of the complex power in an AC circuit, and it is the vector sum of the real power and the reactive power.

While the rated power input can sometimes be similar to the apparent power, especially in simple circuits where the power factor is close to 1, they are not inherently the same. The relationship between the two depends on the specific characteristics of the electrical device or system, including the power factor and any reactive components.

Install my Free Android App on Google Play:

Electrical Cables Most Common Tables “Electrical Cables Tables”

And, my Electrical Calculations App “Fast Electrical Calculator”

Discover more great content by subscribing to My channel

Looking to stay ahead of the game in the world of electrical engineering? Subscribe to my YouTube channel and gain access to exclusive content you won’t find anywhere else!

The staff I recommend

(Amazon Affiliate Links to products I believe are high quality):

Economy 120 Volt/60Hz AC Power Source – Step-Down Voltage & Frequency Converters 1800W
UNI-T Digital Multimeter Tester UT139C
50-Amp Extension Cord for RV “100ft”
Voltage Stabilizer 110/220v
Hair Dryer “best selling“
TOSHIBA EM131A5C-BS Countertop Microwave Ovens

Disclaimer: This contains affiliate links to Amazon products. I may earn a commission for purchases made through these links.