Reactive Power In Power System (Important Facts)

Table of Contents

What Is Reactive Power?

Reactive power can be best described as the unused type of electrical power which is mainly produced in the ac power systems because of the reactive components.

What Causes Reactive Power?

Electrical circuits especially AC circuits have a combination of resistive, inductive, and capacitive elements. Due to the different behaviors, there exists a phase shift between current and voltage.

The amplitude of current and voltage changes continuously. As a result, different forms of power are produced.

Different types of power dissipate in AC circuits i.e. Active power, Reactive, Apparent Power, and complex power.

In the case of pure resistance load (like electrical heaters) only in ac power systems there will be no phase shift between voltage and current then there is only active and apparent power.

Reactive power is 0 VAR in resistive loads

Explaining Reactive Power

As we know Power is the product of voltage (V) and current (I). If any of the elements either current or voltage is zero. The power will be Zero. An AC circuit consists of Elements like a capacitor or inductor.

There will be always a phase shift of 90 Degrees. So, it means that the value of power will be zero when either voltage or current has zero value. It means that the source is generating power but no work is done by the load. Which is not a desirable condition. This is called reactive power.

Sometimes it is called Phantom power, Watt less power, or useless power. It is denoted by Q. And the unit is Volt Ampere (VAR) or KVAR

Formulas and units

AC power system has three types of power, Active, Reactive, and Apparent power. Each one of the three types has its own unit as follows.

Apparent power is measured in Volt Ampere (VA) its formula is S = Voltage * current.
An active power or sometimes is called True power. Its measuring unit is Watt (W). Its mainly consumed in DC circuits and AC resistive loads like heaters.
Reactive or imaginary power. Its measuring unit is Volt Ampere Reactive (VAR). It only appears in AC power systems that have reactive loads like Three and single phase induction motors.

We can use the power factor triangle to memorize the power factor, reactive, apparent, and active power formulas. The triangle is below.

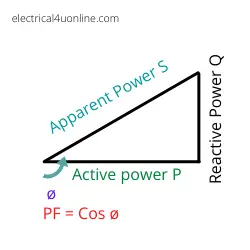
The formula for single phase

The formula for single-phase Reactive Power is given below

Q = V I SinΦ

Where Q Is Power (Reactive in VAR)

V is Voltage

“I” is Current

Φ is the phase angle

The formula for three phase

The formula for three-phase Reactive Power is given below

Reactive Power Q = 1.732 VI sin φ

Other shapes of the formula

Reactive Power Q= √ (S²– P²), While S is apparent power & P is active power.

Why Do we need reactive power in a power system?

In the power system, reactive power is essential. Although it is called useless actually it is not. It is a very important part of electrical power for the purposes of induction, magnetic effect, voltage regulation, and reducing electrical blackouts. I am explaining how all these applications have become possible only because of the presence of reactive power.

Magnetic effect:

As we know that there are 2 types of loads i.e., reactive and non-reactive (resistive) loads. The reactive loads are transformers, motors, and heating systems that run on electricity. These reactive loads need the reactive component of the power to work. If the reactive component of the power is absent then these loads will be unable to do work. Let us say that our power supplier did something magical and made it happen to send pure resistive power to our consumer end from the generation end. Now we started our motor while the motor has no load on it. The motor worked just fine. Then we load the motor and restart it. The motor will not work. The reason is that the motor needs the reactive component of the power to convert the flow of current into something useful. In this particular case, users can be defined as the magnetic flux. Some scenarios will happen with the lamps/ heaters. Lamps and heaters are also reactive loads. They need a reactive component of the power to convert the flow of electrons to induction.

Voltage regulation:

During the transmission, the power supplier can never know the required load value beforehand. The value of the load may increase or decrease at the consumer end. As, the value of the load increases, the required need of the voltage increases and vice versa.

Let’s understand how the reactive component of power helps in providing the rated voltage to the load. Let us assume that the load is more than supplied power. The load will draw more current. So, according to P= V*I, if the value of I increases, the value of V will decrease. But the load also needs the rated voltage to perform normally. So, the reactive component comes in handy in this situation. The regulation devices will detect the problem and increase the value of the reactive voltage in the power. That will help the voltage at the load end to rise to the required rated value.

Now if the load is decreased, the voltage regulator decreases the reactive voltage component in the reactive power. So, the amount of current at the load end does not exceed the rated value.

Satisfying the reactive power needs:

The reactive power is essential to run a loaded motor. We cannot run our motors on a purely resistive power supply. Because a purely resistive power supply cannot produce magnetic induction. So, the devices like transformers and High Voltage DC devices need reactive power to operate.

How does reactive power regulate the voltage of a power system?

Voltage regulation is one of the most important applications of reactive power. The voltage can be regulated with reactive power. During the transmission, the power supplier can never know the required load value beforehand. The value of the load may increase or decrease at the consumer end. As, the value of the load increases, the required need of the voltage increases and vice versa.

Let’s understand how the reactive component of power helps in providing the rated voltage to the load. Let us assume that the load value is more than supplied power. The load will draw more current. So, according to P= VI, if the value of I increases, the value of V will decrease. But the load also needs the rated voltage to perform normally. So, the reactive component comes in handy in this situation. The regulation devices will detect the problem and increase the value of the reactive voltage in the power. That will help the voltage at the load end to rise to the required rated value.

Now if the load is decreased, the voltage regulator decreases the reactive voltage component in the reactive power. So, the amount of current at the load end does not exceed the rated value.

What we have to learn from the discussion above is when the load decreases abruptly, the voltage rises and over-excites the transformer. That leads to damage to the other loads. Also, if the power consumption increases that means if the load increases, it causes the voltage to drop down. That causes a blackout. Reactive power helps us deal with both of these situations. In the case of voltage rise, the power dropped to a lower value by decreasing the reactive component. In the case of voltage drop, the voltage can be increased to the rated value by increasing the reactive component. That is how reactive power regulates the voltage in a system.

How To Reduce Reactive Power In AC Power Systems?

If this type of electrical power is unused, How to reduce it? Well, the answer comes from the power factor triangle. By making power factor corrections. In this way, the active and apparent power should be almost equal.

Improving the PF is done by adding capacitors parallel to the load. Or for large industrial loads, we add an automatic capacitor bank that measures PF and then adds the proper value of capacitors automatically as required by the load PF.

Read also My Article What is Power factor correction?

What Is The Reactive Power Compensation?

The process of managing reactive power in order to improve power consumption is called reactive power compensation.

We have often seen that picture of beer and the lather on the top. The beer in the glass is the active power but the lather is the reactive power.

Real power can be used to work and has a real effect on the power systems. On the other hand, we know that the lather is useless in the glass jar of beer and also takes a space that could be used to fill up with the liquid.

Similarly, reactive power is also useless and takes space in power quantity that could be used. So, we need free up the space that reactive power consumes.

But we cannot get rid of the reactive power as it is needed for the induction process. So, what we can do is to compensate for it.

There are many methods such as Shunt Compensation, Series Compensation, Synchronous Condensers, Static VAR compensators, and Static Compensators.

The shunt compensation device usually known as the shunt compensator is normally connected to the transmission line in parallel to the line. It is connected in the middle of the transmission line.

Shunt-connected compensators (inductive ones) consume the reactive power by reducing the line over-voltage in the transmission line.

On the other hand, the shunt-connected capacitors deliver the reactive power to the line to compensate for reactive power.

Series Compensation is connected in series with the power lines. There are no restrictions for the series compensator to be placed in the middle of the transmission line.

The series compensator can be connected in series with the power transmission line anywhere. It operates in two modes, inductive and capacitive modes.

Static VAR compensator or SVC is the impedance matching machine. Its job is to provide the impedance to the transmission line. It does not have any moving parts, which is why it is called “Static”.

It uses a thyristor-controlled reactor to compensate for the reactive load with the leading or capacitive power factor. On the other hand, the inductive power factor is compensated by switching the capacitor banks, of the compensator, in the system.

A synchronous condenser is also a very good device to deal with the high current due to the reactive power that often leads to the loss of the device. The Synchronous condenser improves the power factor.

The position of the synchronous condenser is normally at the receiving end of the load end. It supplies the reactive power to reduce the current at the load end.

The reduced current cannot overheat the components at the receiving end. So, does not only reduces the reactive power consumption but also is good for the safety and long life of the devices at the load end.

What Are The Advantages Of Reactive Power Compensation?

It is very important to compensate for the reactive power in order to reduce the metal losses. The heat generated in power systems such as generators and transformers due to the reactive power reduces the life of the power systems.

The lagging or leading power factor of reactive power causes the systems to trip or meltdown. By compensating for the reactive power, we save ourselves from the copper losses normally known as the I²R losses.

Also, we save ourselves from periodic changing of the devices. If the power factor is not compensated it reduces the life of devices. So, compensating for the reactive power is really helpful.

How to compensate for reactive power?

There are many methods such as Shunt Compensation, Series Compensation, Synchronous Condensers, Static VAR compensators, and Static Compensators.

Shunt compensation:

The shunt compensation device usually known as the shunt compensator is normally connected to the transmission line in parallel to the line. It is connected in the middle of the transmission line.

Shunt-connected compensators (inductive ones) consume the reactive power by reducing the line over-voltage in the transmission line. On the other hand, the shunt-connected capacitors deliver the reactive power to the line to compensate for reactive power.

Series Compensation:

Series Compensation is connected in series with the power lines. There are no restrictions for the series compensator to be placed in the middle of the transmission line.

The series compensator can be connected in series with the power transmission line anywhere. It operates in two modes, inductive and capacitive modes.

SVC:

Static VAR compensator or SVC is the impedance matching machine. Its job is to provide the impedance to the transmission line.

It does not have any moving parts, which is why it is called “Static”. It uses a thyristor-controlled reactor to compensate for the reactive load with the leading or capacitive power factor.

On the other hand, the inductive power factor is compensated by switching the capacitor banks, of the compensator, in the system.

Synchronous Condenser:

The position of the synchronous condenser is normally at the receiving end or the load end. It supplies the reactive power to reduce the current at the load end.

Does The DC System Have The Active Power Or Reactive Power?

DC power systems only have Active Power. In DC power systems, the reactive power does not exist or is zero.

The reason is that the reactive power comes in present due to the lag of either the current or the voltage. If the current is leading/lagging the phase in a power system, there will be reactive power in the system.

Also, if the voltage is lagging/leading the phase in the power system, the reactive power will come into existence in that system.

But in DC systems, neither the voltage nor the current is out of phase (leading/ lagging the phase). Both quantities are in phase. So, the formula becomes Q_φ = V_φ*I_φ*sinφ, where φ is the phase shift or the difference between the phases of voltage and current. In the case of DC power, φ is 0. So, the term sinφ becomes zero so does the Q_φ.

So, we have also proved mathematically that due to the phase shift i.e., 0 in this case, reactive power becomes zero.

Can Reactive Power Be Negative?

Yes! It is quite normal for the reactive power to be negative. Capacitive loads normally have a negative power factor. Most of the loads have the inductive power factor.

Capacitive and inductive power factors differ by 180 degrees. The reason why we say that the capacitors have negative reactive power is that it cancels the effect of the positive reactive power that exists due to the inductive loads.

Most loads are inductive. One of the easiest ways to understand the reason behind the negative sign of capacitive load is the formula Q = I²X

, where I is the rms value of current and X is the impedance. X is a positive term for the inductor and a negative for the capacitor. I² cannot be negative due to the square of its own. So, the sign of Q, the reactive power, is determined by the sign of X.

Another method, that is a little in-depth, is the mathematical explanation. If we observe the graph of a purely capacitive load, we can see that the real part of the power P is positive for the first half cycle and negative for the last half of the cycle. So, the real power becomes 0. The reactive part of the power is not zero. It is negative.

Another method of explaining the reactive power of the capacitor to be negative is by the power factor. The power factor is found in the average power formula. So, we will understand it using the averaged power formula that is P = V_rmsI_rmscos(ɵ_v– ɵ_i)

, where the term cos(ɵ_v– ɵ_i) is the power factor. If the value of the power factor is negative. That is in RC circuits. Because in the capacitive circuit cos(ɵ_v– ɵ_i) is -90.

The current exists because of the capacitor that provides the voltage and the current leads. When current leads, the power factor becomes negative. As V_rmsI_rms does not play role in the sign of P so it all depends upon the pf. If pf is negative reactive power is going to be negative.

Which Is Greater Reactive or Active Power?

Active power is greater than reactive power. The reason is that without active power, reactive power cannot be useful. If the active power component in power is 0, the reactive power won’t be able to do anything.

But it could also differ on the scenario of the circuit. Let us suppose we have a purely resistive circuit and we are powering it up using AC power.

In this pure resistive circuit, the phenomenon of induction is absent. So, the reactive power is not utilized anywhere. So, the active power will be greater than the reactive power.

Now, let us suppose, we have a purely reactive circuit (inductive or capacitive). Now the active power will not be utilized. So, the reactive power will be greater than the active power.

But we know that both the scenarios explained above cannot be possible in real life. In a real-life scenario, every circuit has reactive as well as resistive components.

And if we keep the definition of work in our minds, then the reactive power is totally useless. But we also know that without reactive power, we will not be able to enjoy the phenomenon of induction.

Why Do We Call Reactive Power Useless?

Reactive power is called useless because it does not do any work. We cannot use only the reactive power to start a device or continuously use the device. We need real power to run the machines.

The statement that reactive power does not do any work needs a little elaboration. We the reactive power starts existing in a circuit, it makes the electrons move back and forth in a fixed position.

We know that in the case of current, the electrons/ holes move from one point to the other to transfer energy. But in the case of reactive power, the electrons do not leave their origin.

They move in to-and-fro motion. So, the work done by the electrons/holes is zero. That is why reactive power is called useless power. But we must keep in mind that in real life we “need” reactive power along with active power to do work.

Does the Generator Produce Reactive Power?

Generators produce active power only. It means that they supply only the voltage. But if the load is inductive, it can supply the current with a phase difference from the phase of the voltage. That will make it look like that the generator is providing the inductive reactive power.

Also, if the load is capacitive, the generator will again produce a voltage and current with a phase difference from the phase of the voltage. That makes it look like that the generator is generating capacitive reactive power. But we must keep in mind that power is really only.

It may behave as reactive but it is not produced like that. Because the load is impedance. Impedance may act as a capacitive load or an inductive load.

The thing we need to remember is that if we over-excite a generator, the generator will provide the capacitive power because capacitive power is being demanded. If the generator is under-excited, that is a normal situation, it acts as an inductive generator because inductive power is being demanded of it.

Now, you might be having trouble understanding if the reactive power is just dependent on the load or if is it possible to produce it. So, the answer is both. If our load is reactive, our generator will automatically change the phase of current and our suppliers will become a reactive supply. The active power is the Cosine function of the power. The Sine function of power is the reactive component of the power.

If we talk about a condenser or a grid-tied synchronous generator, we often find them acting as a capacitor. It is due to the reason that it does not work alone. The voltage that this generator generates is generated a little in advance from the voltage at the grid. This happens when we overexcite the generator.

How To Control The Reactive Power Of A Generator?

First of all, I should make it clear that this question should not be asked by an engineer. If an engineer asks this, he needs to learn a lot. The reactive power generation is not a property of the generator.

If your load is capacitive, the current will automatically change its phase and make a reactive component of the power that runs capacitive loads.

On the other hand, if you remove the capacitive load and connect an inductive load, without any change in the generator component, the generator will provide the power with a reactive component good for the inductive load.

The change should be done at the load end. We know that each ceiling fan has a capacitor, it is to rectify the inductive power factor of the power supplied to the fan.

Because the loads are normally inductive, the power is supplied with an inductive power factor, that needs to be rectified. So, the question is now clear how does the reactive power comes into existence, and if the generator is not doing it how is it existing?

So, the answer is that if we over-excite the generator, the reactive power will be more capacitive. And if we under-excite the generator, it will be more inductive. In both cases, the phase shift is dependent on the load.

Can Reactive Power Affect The Power Factor?

Reactive power has an effect on itself the power factor. If the power factor is 0.95 it means that means we need to provide more reactive power.

But if it is more than 0.95 and is not 1 it means that the power is being utilized more effectively. At the power factor of unity, there is no consumption of reactive power.

At a power factor lesser than 0.95, we have to take care of the fact whether the demanded power is from an inductive load or a capacitive one. Because it depends upon the load only. We can find it by seeing if the power factor is leading or lagging.

For more information about Power Factor, Read My Detailed Article Here?

True / Actual Power vs Reactive Power?

Active power	Reactive power
Active power is the power that is used to do the actual work. To run a motor, light up a bulb, and charge a battery, etc.	Reactive power is not used but is employed to use the phenomenon of induction. Without reactive power, products like transformers would not be able to work.
It is dissipated in resistive components.	It is dissipated in reactive components.
It is denoted by “P”.	It is denoted by “Q”.
It is measured in Watts[W].	It is measured in Volt-Amperes [VA].
In AC circuits, it flows in a direction with a frequency.	In AC circuits, it does not flow but it makes the electrons move back and forth about a mean position.
It cannot produce magnetism.	It produces magnetism.
P= I²R [W]	Q= I²X [VA]

Active vs Reactive Power